“BESARAN DAN SATUAN”
A.Besaran
· Besaran Pokok dan Besaran Turunan
A. Besaran Pokok (Base Quantities)
Besaran yang digunakan dalam fisika dibedakan menjadi dua, yaitu besaran pokok (Base Quantities) dan besaran turunan (Derived Quantities). Besaran pokok adalah besaran adalah besaran yang satuannya didefinisikan terlebih dahulu dan tidak dapat dijabarkan dari besaran lain. Besaran pokok (base Quantities) ada tujuh buah. Ketujuh besaran pokok tersebut dapat kamu lihat pada tabel berikut ini,
No
|
Besaran
|
Satuan
|
Lambang Satuan
|
1.
2. 3. 4. 5. 6. 7. |
panjang
massa waktu suhu kuat arus intensitas cahaya jumlah zat |
meter
kilogram sekon kelvin ampere kandela mol |
m
kg s K A cd mol |
Panjang adalah jarak antara dua titik di dalam ruang. Menurut satuan SI, besaran panjang dinyatakan dalam meter. Satu meter sama dengan jarak yang ditempuh oleh cahaya dalam ruang hampa selama 1/299.792.458 sekon. Besaran panjang diukur dengan menggunakan mistar , stikmeter (meteran gulung), jangka sorong, dan mikrometer skrup. Adapun ketelitian dari masing masing alat tersebut adalah sebagai berikut :
- Mistar (ruler) memiliki ketelitian 1 mm
- stikmeter (measuring tape) memiliki ketelitian 1 mm
- Jangka sorong (Vernier Calipers) ketelitiannya 0,1 mm
- Mikrometer Skrup (micrometer screw gauge) ketelitiannya 0,01 mm
Massa suatu benda adalah banyak zat yang dikandung benda tersebut. Menurut satuan SI, satuan massa adalah kilogram (kg). Dalam kehidupan sehari hari, kita sering menggunakan istilah berat. Misalnya, berat badan Budi 55 kg. Menurut fisika ungkapan tersebut tidak tepat, karena 55 kg adalah massa badan Budi. Berat dalam fisika memiliki pengertian yang berbeda dengan berat dalam kehidupan sehari hari. Menurut fisika, berat adalah gaya yang dialami oleh suatu benda yang mempunyai massa yang diakibatkan karena adanya gaya tarik bumi. Sesuai dengan pengertian ini, maka berat suatu benda di tempat tempat yang berlainan mungkin berbeda beda tergantung besarnya gaya grafitasi di tempat tersebut.
Satu kilogram didefinisikan sebagai massa dari suatu silinder yang dibuat dari campuran platina-iridium yang disebut kiligram standar, yang disimpan di Lembaga berat dan ukuran Internasional di Paris, Perancis. Alat ukur yang digunakan untuk mengukur besaran massa adalah neraca. Terdapat beberapa jenis neraca, antara lain neraca duduk, neraca elektronik, dan neraca lengan.
3. Standar dan Alat Ukur Waktu
Satuan standar untuk waktu adalah seko atau detik. Satu sekon didefinisikan sebagai selang waktu yang diperlukan oleh atom cesium-133 untuk melakukan getaran sebanyak 9.192.631.770 kali. Alat ukur yang digunakan untuk mengukur besaran waktu antara lain arloji dan stopwatch.
4. Standar dan Alat Ukur Suhu
Suhu merupakan derajat panas dinginnya suatu benda. Satuan standar untuk suhu adalah Kelvin. Satuan lain yang sering digunakan di Indonesia adalah derajat Celcius, sedangkan di Amerika dan Inggris pada umumnya menggunakan derajat fahrenheit. Alat untuk mengukur suhu adalah termometer. Untuk mengetahui lebih jauh tentang suhu, akan dibahas lebih rinci pada artikel berikutnya.
B. Besaran Turunan (Derived Quantities)
Besaran turunan adalah besaran yang satuan satuannya diturunkan dari satuan-satuan besaran pokok. Jumlah besaran turunan sangat banyak, semakin berkembangnya ilmu fisika, dimungkinkan akan muncul lagi besaran turunan yang baru. Contoh besaran turunan yang sekarang dikenal dapat kamu lihat pada tabel berikut ini.
No.
|
Besaran
|
Satuan
|
1.
2. 3. 4. 5. 6. 7. |
luas
volume kecepatan gaya massa jenis daya usaha |
meter persegi
meter kubik meter per sekon newton kilogram per meter kubik watt joule |
Pada pembahasan alat ukur sebelumnya, seluruhnya termasuk alat ukur besaran pokok. Bagaimanakan mengukur besaran turunan? Saat ini banyak besaran turunan yang dapat diukur secara langsung, artinya sudah ada alat ukurnya. Misalnya, tekanan udara diukur dengan barometer, gaya diukur dengan dinanometer. dan volume air diukur dengan gelas ukur. Sementara itu untuk mengukur luas atau volume suatu benda yang bentuknya beraturan kita dapat menggunakan rumus matematika. Ayo buka lagi pelajaran Matematika SD yang sudah kamu pelajari. Lalu bagaimana jika benda yang akan kita ukur bentuknya tidak beraturan, misalnya saja batu? untuk mengukurnya kita dapat menggunakan gelas ukur. Oke deh sampai disini dulu ya pembahasannya, Selamat belajar, SUKSES !
Pengertian
Satuan
Satuan
didefinisikan sebagai pembanding dalam suatu pengukuran besaran. Setiap besaran
mempunyai satuan masing-masing, tidak mungkin dalam 2 besaran yang berbeda
mempunyai satuan yang sama. Apa bila ada dua besaran berbeda kemudian mempunyai
satuan sama maka besaran itu pada hakekatnya adalah sama. Sebagai contoh Gaya
(F) mempunyai satuan Newton dan Berat (w) mempunyai satuan Newton. Besaran ini
kelihatannya berbeda tetapi sesungguhnya besaran ini sama yaitu besaran turunan
gaya. Untuk melihat berbagai rumus dalam bab besaran dan satuan silakan klik Besaran
berdasarkan arah dapat dibedakan menjadi 2 macam
- Besaran vektor adalah besaran yang mempunyai nilai dan arah sebagai contoh besaran kecepatan, percepatan dan lain-lain.
- Besaran sekalar adalah besaranyang mempunyai nilai saja sebagai contoh kelajuan, perlajuan dan lain-lain.
VEKTOR
BESARAN VEKTOR
A. Menggabungkan atau Menjumlahkan Besaran vektor
a. Secara
Grafis
1. Metode
Poligon
Penggabungan vektor secara
poligon dilakukan dengan cara menggambar vektor-vektor yang digabungkan
tersebut secara berurutan (diteruskan). Kemudian Vektor resultannya (R)
digambar dengan menghubungkan titik awal sampai akhir.
2. Metode
Jajaran genjang
Penggabungan vektor secara
jajaran genjang dibuat dengan cara menggambar vektor-vektor yang akan
digabungkan dari titik awal yang sama, kemudian buatlah garis sejajar vektor
tadi (garis putus-putus) dari kedua ujung vektor yang digabungkan sehingga
diperoleh titik potongnya. Terakhir gambarlah Vektor Resultannya dengan
menghubungkan titik awal ke titik potong.
b. Secara
Analitis (Perhitungan)
1. Jika
arahnya sama
Resultan vektor yang arahnya
sama dihitung dengan menjumlahkan besar dari kedua vektor yang digabungkan.
R = V1 + V2
2. Jika
arahnya berlawanan
Resultan vektor yang arahnya
sama dihitung dengan mengurangkan besar dari kedua vektor yang digabungkan
(dihitung selisihnya).
R = V1 - V2
3. Jika
saling mengapit sudut
Resultan dari vektor yang
arahnya tidak sama dan tidak berlawanan atau arahnya saling mengapit sudut
dihitung dengan menggunakan rumus sbb :
Contoh Soal
:
- Vektor Fa dan Fb berturut-turut 30 N dan 50 N. Berapa resultan kedua vektor tersebut jika :
a.
kedua vektor searah !
b. kedua
vektor berlawanan arah !
c. kedua
vektor saling mengapit sudut 60° !
Diketahui
:
Fa = 30 N
Fb = 50 N
Ditanyakan
: a) R = ................. ? (searah)
b) R = ................. ? (berlawanan arah)
c) R = ................. ? α = 60°
a) R
= Fa + Fb
b) R = Fa - Fb
R = 30 + 50
R = 30 - 50
R = 80
N
R = - 20 N
(tanda – menyatakan arah R sama dengan Fb)
2.
Vektor V = 400 N dengan arah 30° terhadap arah horizontal.
Tentukan komponen vektor diatas pada sumbu X dan sumbu Y !
Diketahui : V = 400 N
Ditanyakan : Vx = .................. ?
Vy = ................. ?
Vx = V Cos
α
Vy = V Sin α
Vx = 400 Cos 30°
Vy = 400 Sin 30°
Vx = 400
0,87
Vy = 400 0,5
Vx = 348
N
Vy = 200 N
B. Menguraikan Besaran Vektor
Perhatikan vektor P pada gambar dibawah !
Arah vektor P adalah ke kanan atas, vektor ini dapat
diuraikan menjadi dua komponen yaitu (Px) ke kanan dan (Py) ke atas seperti
pada gambar.
Contoh 1
Sebuah vektor P mempunyai besar 200 satuan dengan arah
membentuk sudut 30 ˚ dengan sumbu X positif. Berapakah besar komponen vektor
diatas pada sumbu X dan pada sumbu Y ?
Diketahui : P = 200 satauan
α = 30˚
Diatanya : Px ..... ?
Py ..... ?
a. Px = P Cos
α
b. Py = P Sin α
Px = 200 Cos
30˚
Py = 200 Sin 30˚
Px = 200 . 0,5√3
Py = 200 . 0,5
Px = 100 √3
satuan
Py = 100 satuan
Contoh 2
Komponen dari vektor A pada sumbu X adalah 150 satuan. Bila vektor A mengapit
sudut 60˚ dengan sumbu X positif. Berapakah besar komponen vektor A pada sumbu
Y dan berapa pula besar vektor A tersebut ?
Diketahui : Ax = 150 satuan
α = 60˚
Ditanya : Ay .......... ?
A ............. ?
a. Ax
= A Cos α
b. A2 = (Ax)2
+ (Ay)2
150 = A Cos 60˚
3002 = 1502 + (Ay)2
150 = A .
0,5
90000 = 22500 + (Ay)2
A = 150 / 0,5
(Ay)2 = 90000 - 22500
A = 300 satuan
(Ay)2 = 67500
Ay = √67500 satuan
C. Perkalian
Besaran Vektor
1. Dot
Produck (Perkalian vektor dengan vektor hasilnya skalar)
Misalnya F(vektor gaya) dan S (vektor perpindahan), Jika kedua vektor
diatas dikalikan hasilnya akan berupa sebuah sekalar yaitu W (Usaha). Secara
Matermatika Dot Produck dapat ditulis :
V1 . V2 =
V1.V2 Cos α
2. Kros
Produck (perkalian vektor dengan vektor hasilnya vektor)
Misalnya F (vektor gaya) dan R (vektor posisi), jika keuda vektor tersebut
dikalikan hasilnya akan berupa sebuah vektor baru yaitu τ (Momen Gaya). Secara
Matematika perkalian Kros Product dapat ditulis sbb :
V1 x V2 = V1.V2
Sin α
Arah dari hasil perkalian vektor dengan cara kros
product dapat ditentukan dengan aturan putaran skrup, yaitu putaran skrup sama
dengan arah putaran vektor melalui sudut terkecil sedangkan arah gerakan skrup
menyatakan arah vektor yang dihasilkan dari perkalian kros product.
GERAK LURUS
Suatu benda melakukan gerak, bila
benda tersebut kedudukannya (jaraknya) berubah setiap saat terhadap titik
asalnya ( titik acuan ).
Sebuah benda dikatakan bergerak
lurus, jika lintasannya berbentuk garis lurus. Contoh : - gerak jatuh bebas
- gerak mobil di jalan.
Gerak
lurus yang kita bahas ada dua macam yaitu :
1.
Gerak lurus beraturan (disingkat GLB)
2.
Gerak lurus berubah beraturan (disingkat
GLBB)
Definisi
yang perlu dipahami :
1.
KINEMATIKA ialah ilmu yang mempelajari gerak tanpa
mengindahkan penyebabnya.
2.
DINAMIKA ialah ilmu yang mempelajari gerak
dan gaya-gaya penyebabnya.
-
JARAK merupakan panjang lintasan yang
ditempuh oleh suatu materi (zat)
-
PERPINDAHAN ialah perubahan posisi
suatu benda yang dihitung dari posisi awal
(acuan)benda tersebut
dan tergantung pada arah geraknya.
a. Perpindahan POSITIF
jika arah gerak ke KANAN
b. Perpindahan NEGATIF
jika arah gerak ke KIRI
GERAK LURUS BERUBAH BERATURAN ( GLB )
Gerak
lurus beraturan ialah gerak dengan lintasan serta kecepatannya selalu tetap.
KECEPATAN
( v ) ialah besaran vektor yang besarnya sesuai dengan perubahan lintasan
tiap
satuan waktu.
KELAJUAN ialah besaran skalar yang besarnya sesuai dengan
perubahan lintasan tiap
satuan
waktu.
Pada Gerak Lurus Beraturan (
GLB ) berlaku rumus : x = v . t
dimana
: x = jarak yang ditempuh ( perubahan lintasan )
v = kecepatan
t = waktu
Gerak Melingkar
Gerak
melingkar merupakan gerak benda yang lintasannya membentuk lingkaran.
Banyak contoh gerak melingkar dalam kehidupan sehari-hari, seperti
gerakan komidi putar, gerak bandul yang diayunkan berputar, pelari yang
mengelilingi lapangan berbentuk lingkaran, atau gerakan akrobatik di
pasar malam "tong stan". Jika anda menggambar sebuah bangun berupa
lingkaran, maka gerakan pena anda merupakan gerak melingkar. Pada bab
ini kita akan mengenal besaran-besaran yang berlaku dalam gerak
melingkar yaitu, frekuensi putaran, periode putaran, kecepatan linier,
kecepatan sudut, dan percepatan sentripetal. Secara khusus kita akan
membahas dua gerak melingkar yaitu gerak melingkar beraturan dan gerak
melingkar berubah beraturan.
A. Gerak Melingkar Beraturan.
Benda
dikatakan bergerak melingkar beraturan jika lintasannya berupa
lingkaran dengan kelajuan tetap,.ingat bukan kecepatan tetap. Hal ini
dapat dijelaskan melalui gambar berikut,
Pada
gambar di atas kelajuan materi dititik A, B, C dan D bernilai sama atau
tetap. Namun arahnya di setiap titik tersebut berbeda. Hal inilah yang
membedakan antara laju dan kecepatan gerak benda melingkar. Kecepatan di
A dengan arah ke atas, kecepatan di titik B arah ke kiri, kecepatan di
titik C arah ke bawah dan kecepatan di D arah ke kanan.
Beberapa besaran pada gerak melingkar beraturan
1. Periode dan Frekuensi
Periode (T) putaran sebuah benda didefinisikan sebagai waktu yang diperlukan untuk satu kali putaran. Jika untuk menempuh satu kali putaran diperlukan waktu 5 sekon maka boleh dikatakan periode putaran benda (T) tersebut adalah 5 sekon. Jika untuk menempuh n putaran diperlukan waktu selama t sekon, maka periode benda dapat dinyatakan dalam persamaan sebagai berikut :
Dimana :
T = periode (sekon)
t = waktu selama putaran (sekon)
n = banyaknya putaran
Frekuensi (f) adalah banyaknya putaran persatuan waktu. Jika sebuah roda berputar pada porosnya 10 kali putaran selama 5 sekon maka frekuensi perputaran roda tersebut sebesar 2 Hz. Jika untuk melakukan n putaran memerlukan waktu t sekon maka frekuensi dapat dinyatakan dalam persamaan :
Hubungan antara periode (T) dan frekuensi dinyatakan dalam persamaan berikut :
atau :
Contoh soal : Periode (T) putaran sebuah benda didefinisikan sebagai waktu yang diperlukan untuk satu kali putaran. Jika untuk menempuh satu kali putaran diperlukan waktu 5 sekon maka boleh dikatakan periode putaran benda (T) tersebut adalah 5 sekon. Jika untuk menempuh n putaran diperlukan waktu selama t sekon, maka periode benda dapat dinyatakan dalam persamaan sebagai berikut :
Dimana :
T = periode (sekon)
t = waktu selama putaran (sekon)
n = banyaknya putaran
Frekuensi (f) adalah banyaknya putaran persatuan waktu. Jika sebuah roda berputar pada porosnya 10 kali putaran selama 5 sekon maka frekuensi perputaran roda tersebut sebesar 2 Hz. Jika untuk melakukan n putaran memerlukan waktu t sekon maka frekuensi dapat dinyatakan dalam persamaan :
Hubungan antara periode (T) dan frekuensi dinyatakan dalam persamaan berikut :
atau :
Sebuah materi melakukan gerak melingkar selama 5 menit. Jika dalam waktu tersebut , materi telah melakukan 600 putaran maka frekuensi dan periode putaran materi tersebut adalah....
Solusi :
Materi telah melakukan 600 putaran (n) selama 5 menit = 5 x 60 sekon = 300 sekon (t), maka :
a. f = n/t = 600/300 = 2 Hz
b. T = t/n = 300/600 = 0,5 sekon
atau untuk mencari T = 1/f, sehingga T = 1/2 sekon.
2. Kecepatan sudut dan kecepatan linier
Kecepatan sudut didefinisikan sebagai besar sudut yang ditempuh tiap satu satuan waktu. Dalam gerak melingkar beraturan, kecepatan sudut atau kecepatan anguler untuk selang waktu yang sama selalu konstan. Untuk partikel yang melakukan gerak satu kali putaran, berarti sudut yang ditempuh adalah 360 derajat atau 2 pi dan waktu yang diperlukan untuk satu kali putaran disebut satu periode (T). Maka kecepatan sudut dapat dinyatakan dalam persamaan berikut :
Hubungan antara kecepatan sudut dengan kecepatan linier dapat dinyatakan dalam persamaan berikut :
Karena
Maka :
Hukum Newton
A. Hukum I Newton
“Jika resultan gaya
yang bekerja pada benda sama dengan nol maka benda yang mula-mula diam
akan tetap diam dan benda yang mula-mula bergerak lurus beraturan akan
tetap bergerak lurus beraturan.”
Untuk mengetahui demontrasi hukum newton I, ini contoh prakteknya ada
seorang aank yang menarik dengan cepat vas bunga maka vas bunga
akantetap di atas meja

Hukum Newton I juga dapat dinyatakan bila
sebuah benda dalam keadaan diam maka benda itu akan tetap diam dan jika
bergerak dengan kecepatan tetap akan terus bergerak dengan kecepatan
tetap contohnya sebagai berikut :
Ketika kita naik motor tiba-tiba di rem mendadak maka akan terdorong ke belakang
2. Ketika kita nenarik kertas dengan cepat maka uang diatas kertas seperti gambar disamping akan tetap ditempatnya
2. Ketika kita nenarik kertas dengan cepat maka uang diatas kertas seperti gambar disamping akan tetap ditempatnya
Apabila resultan gaya yang bekerja pada sebuah benda tidak sama dengan nol maka benda tersbut akan bergerak dengan sebuah percepatan.
Besarnya percepatan suatu benda sebanding dengan
resultan gayanya. Semakin besar resultan gaya yang bekerja pada suatu
benda, percepatannya akan semakin besar. Apabila percepatan disimbolkan
dengan a dan resultan gaya disimbolkan dengan ∑F, dapat dituliskan
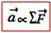
Untuk
resultan gaya tetap yang bekerja pada suatu benda dengan massa semakin
besar, semakin kecil percepatan yang terjadi. Apabila massa kelembaman
benda disimbolkan dengan m, diperoleh hubungan percepatan dan massa
sebagai berikut.
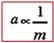
Percepatan dihasilkan oleh suatu resultan yang
bekerja pada suatu benda berbanding lurus dengan resultan gaya, searah
dengan resultan gaya dan berbanding terbalik dengan massa benda. Secara
matematis hukum II Newton dirumuskan
Rumusan gayaPercepatan dihasilkan olehsuaturesultan yang bekerjapadasuatubenda berbandinglurusdenganresultangaya, searahdenganresultangayadanberbandingterbalikdenganmassabenda. Secaramatematishukum II Newton dirumuskan :
Rumusan gayaPercepatan dihasilkan olehsuaturesultan yang bekerjapadasuatubenda berbandinglurusdenganresultangaya, searahdenganresultangayadanberbandingterbalikdenganmassabenda. Secaramatematishukum II Newton dirumuskan :
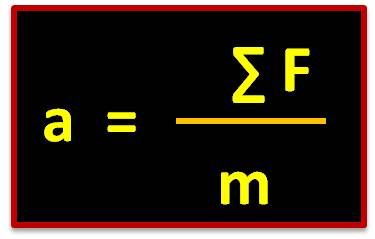
atau bisa juga ditulisakan sebagai berikut ini :

F = Gaya satuuanya Newton ( N )
m= massa benda satuannya kilogram ( kg )
a = percepatansatuanya (m/s2 )
C. Hukum III Newton
Jika benda A gaya pada benda B( gaya aksi ), maka
benda B juga akan memberikan gaya pada benda A ( gaya reaksi ). Kedua
gaya tersebut mempunyai besar yang sama tetapi mempunyai arah yang
berlawanan. Kedua gaya aksi dan reaksi tersebut bekerja pada benda yang
berbeda. Pernyataan hukum III Newton dalam persamaan dinyatakan sebagai
berikut : F aksi = - F reaksi
contoh penerapan hukum Newton III adalah ketika kita sedang meluncurkan roket air maka roket air dapat meluncur ke atas karena ada gaya dorong air ke bawah. contoh lain adalah ketika kita sedang berenang ketika kita ingin bergerak maju ke depan maka kita mengayunkan tangan ke belakang.
contoh penerapan hukum Newton III adalah ketika kita sedang meluncurkan roket air maka roket air dapat meluncur ke atas karena ada gaya dorong air ke bawah. contoh lain adalah ketika kita sedang berenang ketika kita ingin bergerak maju ke depan maka kita mengayunkan tangan ke belakang.
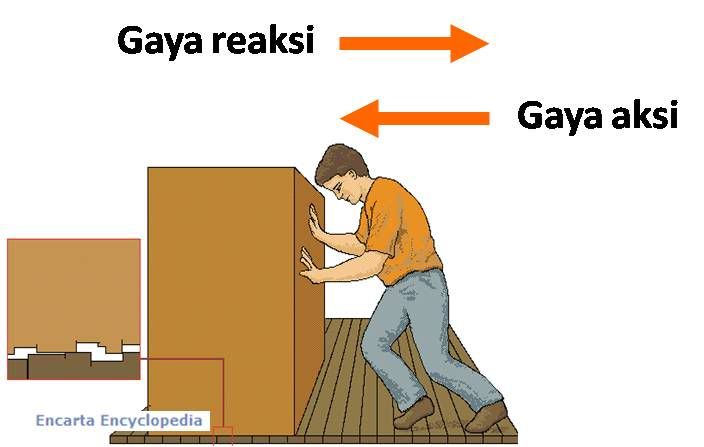 |
| Gambar gaya aksi dan reaksi |
 |
| Sir Isac Newton |
Sir Isaac Newton adalah ahli fisika,
matematika, astronomi, kimia dan ahli filsafat yang lahir di Inggris.
Isaac Newton menyadari bahwa matematika adalah cara untuk menjelaskan
hukum-hukum alam seperti gravitasi, dan membuat beberapa rumus untuk
menghitung 'pergerakan benda' dan 'gravitasi bumi'. Gravitasi adalah
kekuatan yang membuat suatu benda selalu bergerak jatuh ke bawah. Dengan
tiga prinsip dasar dari hukum pergerakan, Newton dapat menjelaskan dan
membuktikan bahwa planet beredar mengelilingi matahari dalam orbit yang
berbentuk oval dan tidak bulat penuh. Kemudian Newton menggunakan tiga
prinsip dasar pergerakan yang sekarang di kenal sebagai Hukum Newton
untuk menjelaskan bagaimana benda bergerak.
Saat ini banyak kisah yang menceritakan bahwa
Newton mendapatkan rumus tentang teori gravitasi dan sebuah apel yang
jatuh dari pohon. Di kisahkan bahwa suatu hari Newton duduk dan belajar
di bawah pohon apel dan saat itu sebuah apel jatuh dari pohon tersebut.
Dengan mengamati apel yang jatuh, Newton mengambil kesimpulan bahwa ada
sesuatu kekuatan yang menarik apel tersebut jatuh kebawah, dan kekuatan
itu yang kita kenal sekarang dengan nama gravitasi.
Memadu Gerak
1. Perpaduan gerak antara GLB dan GLB
Bila dua buah gerak GLB saling dipadukan, ternyata hasil perpaduannya juga
menghasilkan GLB.
Penerapan yang umum adalah gerak perahu menyeberangi sungai yang memotong
tegak lurus aliran arus sungai.
Besar Kecepatan
Resultan :
Kecepatana tetap ( GLB) = Vx Dimana
:
Kecepatan beraturan (GLB) = Vy
Catatan : hasil perpaduan GLB
dan GLB adalah GLB juga
- Perpaduan gerak antara GLB dan GLBB
- Bila dua buah gerak, GLB dan GLBB saling dipadukan, ternyata hasil perpaduannya menghasilkan gerak yang berbeda, tidak GLB maupun GLBB.
- Hasil perpaduan ini menghasilkan Gerak Parabola atau dikenal dengan Gerak Peluru, karena lintasannya seperti peluru yang ditembakka.
GERAK PARABOLA
Dalam Gerak
Parabola, akan kita bahas :
l Kecepatan
dalam arah sumbu x dan y
l Vektor,
Besar dan Arah Kecepatan
l Waktu
untuk mencapai titik tertinggi dan titik terjauh
l Koordinat
titik tertinggi dan titik terjauh (x,y)
l Kecepatan
pada titik terjauh
l Dan sebagainya








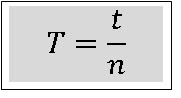
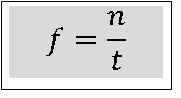




No comments:
Post a Comment